1. Quelques basiques#
1.1 Types de données#
| Quantitatives | Définition | Exemple |
|---|---|---|
| Continues | prend n’importe quelle valeur dans un ensemble de valeurs | température, prix, taux de chômage, … |
| Discrètes | ne prend qu’un nombre limité de valeurs dans un ensemble de valeurs | nombre de personnes dans un ménage, nombre de pièces dans une maison, … |
| Qualitatives | Définition | Exemple |
|---|---|---|
| Nominales (catégorielles) | ne peut pas être ordonnées | sexe, couleur, ville, … |
| Ordinales | sont classées dans un ordre logique et que l’on trouve principalement dans les questionnaires demandant une opinion | d’accord, neutre, pas d’accord |
1.2. Types d’algorithmes#
| Supervisés | ||
|---|---|---|
| Définition | Ils sont formés sur un ensemble de données étiquetées, où chaque exemple de formation est associé à une étiquette ou à une sortie souhaitée | |
| Objectif | L’objectif est d’apprendre une correspondance entre les entrées et les sorties, en utilisant ces exemples étiquetés pour prédire les sorties pour de nouvelles entrées. | |
| Exemple | régression linéaire, régression logistique, arbres de décision, réseaux neuronaux, etc | |
| Applications | classification, régression, prédiction |
| Non supervisé | ||
|---|---|---|
| Définition | Ils sont utilisés sur des ensembles de données non étiquetés, où les exemples d’apprentissage ne sont pas associés à des étiquettes de sortie | |
| Objectif | L’objectif est de découvrir des structures ou des modèles sous-jacents dans les données, souvent sans aucune indication préalable des résultats attendus. | |
| Exemple | k-means, analyse en composantes principales (ACP), regroupement hiérarchique, etc. | |
| Applications | regroupement, réduction de la dimensionnalité, détection d’anomalies |
1.3. Régression vs. classification#
Cette distinction ne s’applique qu’aux algorithmes supervisés, et plus particulièrement au type de données de sortie Y.
- Régression : les données de Y peuvent prendre une infinité de valeurs continues (par exemple, prix, PIB, taux de chômage, etc.).
- Classification : les données Y sont des nombres finis, parfois appelés « étiquettes » (par exemple, « oui/non » (valeurs binaires) ou « S/M/L »).
2. Algorithmes supervisés#
2.1. Régression linéaire (univariée et multivariée)#
Dans la régression linéaire, le modèle dépend d’une ou plusieurs variables explicatives \(X\), qui correspondent aux entrées. En utilisant ces valeurs \(X\), nous recherchons la meilleure fonction d’hypothèse pour approximer les valeurs de sortie \(Y\). Pour la trouver, nous devons minimiser la fonction d’hypothèse.
Pour la trouver, nous devons minimiser sa fonction de coût \(J\), qui est la somme normalisée des erreurs de la fonction d’hypothèse. En d’autres termes, l’estimation du coefficient est basée sur la minimisation de la variance résiduelle.
$$Y = \beta_0 + \beta_1X + \beta_2X + \dots + \beta_nX + \epsilon$$
2.2. Régression polynomiale#
Il s’agit d’une extension de la régression linéaire multivariée en ce sens qu’elle peut être utilisée pour traiter des données ayant une tendance non linéaire, c’est-à-dire avec des polynômes de degré supérieur à 1.
En pratique, les calculs sont les mêmes que pour la régression linéaire, cette dernière étant simplement une régression polynomiale de degré 1.
Fondamentalement, le modèle de régression tente de s’adapter à une courbe plutôt qu’à une ligne droite.
$$Y = \beta_0 + \beta_1X^1 + \beta_2X^2 + \dots + \beta_nX^n + \epsilon$$
2.3. Régression régularisée#
La régression régularisée consiste à ajouter des termes de régularisation à la fonction de coût afin de contrôler la complexité du modèle et de réduire l’ajustement excessif en empêchant des valeurs trop grandes et amener les solutions autour de 0.
En effet, des paramètres avec de grandes valeurs forment des zones très étendues qui peut générer des arêtes ou des vallées. On parle de risque d’instabilité.
Deux types de régression régularisée sont couramment utilisées :la régression LASSO (Least Absolute Shrinkage and Selection Operator) (\(l_1\)).
Régression Ridge - \(l_2\)#
On limite l’instabilité liée à des variables explicatives trop corrélées entre elles en utilisant la distance euclidienne comme norme du vecteur des paramètres :
$$P(\lambda, \beta) = \lambda\sum^p_{j=1}\beta_j^2$$
$$Y = \beta_0 + \beta_1X + \beta_2X_2 + \dots + \beta_pX_p + P(\lambda, \beta) + \epsilon$$
Régression LASSO - \(l_1\)#
(Least Absolute Shrinkage and Selection Operator) Le principe est identique à la régression ridge mais la norme utilisée ici est la distance de Manhattan :
$$P(\lambda, \beta) = \lambda\sum^p_{j=1}|\beta_j^2|$$
$$Y = \beta_0 + \beta_1X + \beta_2X_2 + \dots + \beta_pX_p + P(\lambda, \beta) + \epsilon$$
Cette méthode a l’avantage de simplifier le modèle en éliminant des variables.
Avec \(\lambda\) le paramètre de régularisation qui contrôle l’intensité de la régularisation et \(\epsilon\) l’erreur résiduelle.
2.4. Classificateur - Naive Bayes#
Naive Bayes est un classificateur relativement simple, basé sur l’hypothèse forte que chaque paire de variables est indépendante.
Étant donné \(N\) variables \((X_1, X_2, \dots, X_n)\) prenant des valeurs \(x_{ij}\) sur la base desquelles nous cherchons à prendre une décision binaire \(d \in \N\{0,1\}\), nous calculons le rapport de probabilité \(A\) par :
$$ A = \prod_{i=1}^n\frac{p(x_i | d=1)}{p(x_i | d=0)} \times \frac{p(d=1)}{p(d=0)} $$
… avec une décision $$d=1 \text{ si } A > \alpha$$ $$d=0 \text{ si } A \le \alpha$$
2.5. Classificateur - Régression logistique#
Le modèle de régression logistique est basé sur une fonction logistique (ou sigmoïde) qui transforme la somme pondérée des caractéristiques d’une observation en une probabilité que cette observation appartienne à une classe particulière.
Mathématiquement, pour la régression logistique binaire, la fonction logistique est définie comme suit :
$$p(y=1|X) = \frac{1}{1+\epsilon^{-(\beta_0 + \beta_1X_1 + \beta_2X_2 + \dots + \beta_pX_p)}}$$
Le modèle de régression logistique est entraîné pour estimer les coefficients \(\beta_0, \beta_1, \dots, \beta_p\), qui maximisent la vraisemblance des données observées.
Une fois les coefficients estimés, le modèle peut être utilisé pour prédire la probabilité d’appartenance à chaque classe pour de nouvelles observations.
2.6. Random Tree & Random Forest#
Random Tree#
- Apprendre des décisions à partir de données en formant une structure arborescente
- Chaque nœud de l’arbre représente une caractéristique des données, chaque arête représente une décision basée sur cette caractéristique et chaque feuille de l’arbre représente une classe ou une valeur de prédiction.
- Les arbres de décision sont faciles à interpréter et à visualiser, ce qui les rend utiles pour comprendre les relations entre les caractéristiques et la variable cible.
- Toutefois, ils peuvent être sujets à un surajustement lorsqu’ils sont trop profonds et trop complexes. Cela peut être évité en utilisant des techniques telles que la taille maximale de l’arbre, la taille minimale de l’échantillon pour diviser un nœud, etc.
Random Forest#
- Il s’agit d’ensembles d’arbres de décision.
- Chaque arbre de la forêt est formé sur un échantillon aléatoire de données (bootstrap) et utilise un sous-ensemble aléatoire de caractéristiques pour former divers arbres.
- Les prédictions des arbres individuels sont ensuite agrégées (par vote majoritaire pour la classification ou par moyenne pour la régression) pour produire une prédiction finale.
- Les forêts aléatoires sont très robustes, moins sensibles à l’ajustement excessif que les arbres de décision individuels, et offrent généralement de meilleures performances prédictives.
- Elles sont particulièrement efficaces pour gérer des ensembles de données complexes comportant de nombreuses caractéristiques et des relations non linéaires entre les caractéristiques et la variable cible.
Les avantages de ces méthodes : non paramétriques et non linéaires.
2.7. Gradient boosting#
L’amplification du gradient est une technique d’apprentissage automatique qui construit un modèle prédictif en ajoutant itérativement des modèles d’apprentissage faibles, généralement des arbres de décision peu profonds, pour corriger les erreurs du modèle précédent.
Cette méthode est connue sous le nom de « boosting », car chaque modèle ajouté est formé pour améliorer les performances du modèle global. Ces mises à jour sont effectuées par le biais du gradient de la fonction de coût choisie.
L’assemblage final est une combinaison linéaire de chacun des algorithmes faibles, ceux qui produisent l’erreur la plus faible étant surpondérés au cours de l’assemblage.
2.8. Support Vector Machine (SVM)#
Le SVM est un puissant algorithme d’apprentissage supervisé utilisé pour la classification et la régression.
Il est particulièrement bien adapté à la séparation de données dans des espaces à haute dimension, offrant une grande robustesse et de hautes performances.
L’une des principales forces des SVM réside dans leur capacité à trouver un hyperplan de séparation qui maximise la marge entre les classes, ce qui permet une meilleure généralisation et réduit le risque de surajustement.
En outre, les SVM peuvent traiter efficacement des données non linéaires grâce à l’utilisation de noyaux, ce qui permet de projeter les données dans des espaces de plus grande dimension où la séparation linéaire est possible.
Grâce à sa capacité à traiter des ensembles de données à haute dimension et à sa flexibilité dans le choix des noyaux, le SVM est un choix populaire pour de nombreux problèmes de classification et de régression dans divers domaines.
3.Algorithmes non supervisés#
3.1. Clustering#
Un bon clustering doit créer des groupes d’individus présentant les caractéristiques suivantes
- une forte similarité intra-classe, c’est-à-dire qu’ils doivent être similaires
- une faible similarité interclasse, c’est-à-dire que les groupes sont assez distincts les uns des autres.
Pour y parvenir, il existe deux approches du clustering.
Clustering hiérarchique#
- Elle peut être ascendante ou descendante. La plus répandue est l’approche ascendante.
- Les classes sont construites par agglomérations successives d’objets deux à deux : les distances entre chaque point sont calculées, les deux points les plus proches sont agglomérés et le processus est répété jusqu’à ce qu’il ne reste plus que le groupe entier.
- En d’autres termes, on commence par calculer les feuilles et on remonte jusqu’à la racine de l’arbre, appelée dendrogramme.
- Enfin, le dendrogramme est interprété en le tronquant, ce qui permet de séparer les groupes.
Clustering non-hiérarchique#
- L’objectif est similaire à celui du clustering hiérarchique, sauf que le nombre total de clusters est connu à l’avance.
- L’algorithme des centres mobiles est généralement utilisé : On détermine au hasard \(k\) centres provisoires de grappes et on note ces grappes.
- L’opération est répétée plusieurs fois jusqu’à ce qu’un équilibre soit stabilisé.
3.2. Analyse factorielle#
PCA - Principal Component Analysis#
- Technique statistique utilisée pour réduire la dimensionnalité des données en les projetant dans un espace plus restreint de variables, tout en préservant autant que possible leur variance.
- Visualiser et interpréter les relations entre les variables
- Détecter des modèles ou des tendances cachées
- Simplifier la complexité des données et faciliter leur analyse.
- Analyse entre variables quantitatives.
LDA - Linear Discriminant Analysis#
- Méthode statistique permettant d’analyser et d’interpréter les différences entre plusieurs groupes ou classes prédéfinis sur la base de variables continues.
- Contrairement à la PCA qui vise à maximiser la variance totale des données, la LDA cherche à maximiser la séparation entre les groupes tout en minimisant la variance à l’intérieur de chaque groupe.
- Elle peut donc être utilisée pour identifier les variables les plus discriminantes entre les groupes et pour classer de nouveaux individus dans des groupes existants sur la base de leurs caractéristiques.
- Cette méthode est équivalente à la régression linéaire, mais pour une variable dépendante qualitative \(y\).
CFA - Correspondence Factor Analysis#
- Méthode d’analyse statistique largement utilisée pour explorer la structure des relations entre les variables catégorielles.
- Elle permet de détecter des associations entre les modalités de différentes variables et de les représenter graphiquement dans un espace de dimensions réduites.
- La CFA est particulièrement utile pour analyser les tableaux de contingence, c’est-à-dire les tableaux croisés entre plusieurs variables qualitatives.
- Elle peut être utilisée pour visualiser les relations entre les catégories de variables et pour identifier les tendances ou les regroupements au sein des données.
MCA - Multiple Correspondence Analysis#
- Il s’agit d’une extension de l’AFC qui permet d’analyser simultanément plusieurs tableaux de contingence.
- Contrairement à la CFA qui ne peut traiter qu’un seul tableau de contingence à la fois, la MCA peut prendre en compte plusieurs tableaux croisés entre différentes variables catégorielles.
- Cette méthode permet d’étudier des relations complexes entre plusieurs ensembles de variables qualitatives et de les représenter dans un espace de dimensions réduites.
- La MCA est utile lorsque les données contiennent plusieurs sources de variation et que l’on souhaite identifier des structures communes ou spécifiques entre différents groupes de variables.
4. Deep Learning (ou réseaux neuronaux)#
Les réseaux de neurones sont des simulations informatiques du cerveau humain, conçues pour reproduire certaines capacités humaines complexes (compréhension, reconnaissance, raisonnement à partir d’informations partielles, etc.)
L’apprentissage par ces réseaux peut être supervisé si on leur fournit une base de données (reconnaissance de caractères) ou non supervisé lorsque le réseau apprend de ses erreurs (un robot qui apprend à marcher).
La structure d’un réseau neuronal peut être illustrée comme suit :
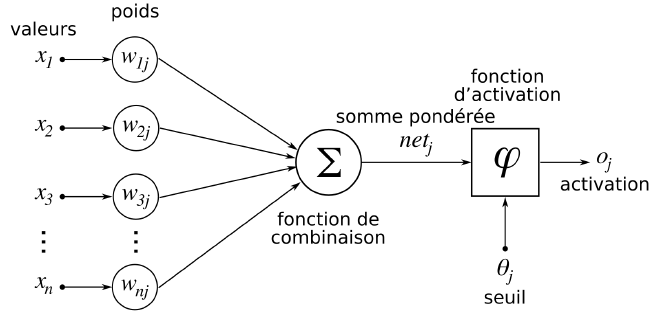
Voici ses caractéristiques :
- Les valeurs \(x_1\), \(x_2\), … représentent les données entrées dans le réseau neuronal.
- Les coefficients de pondération \(w_{1j}\), \(w_{2j}\), … sont automatiquement attribués par le réseau neuronal à chacune des données en fonction des informations qu’elle contient.
- Toutes ces valeurs et leurs coefficients construisent une fonction de combinaison linéaire \(\Sigma\) dont la somme sera pondérée.
- Les fonctions d’activation \(\varphi\) prennent la forme d’une fonction que l’on définit (sigmoïde, tangente hyperbolique, linéaire, …) jusqu’à un certain seuil \(\theta_j\)
- A la sortie, on a l’activation \(o_j\)
La formule d’apprentissage des neurones est définie par :
$${P_{k+1} = P_k - \text{step} \times \nabla J (P_k)}$$
… avec le vecteur de poids :
$$P = \begin{pmatrix} w_1 \newline w_2 \newline \vdots \newline w_n \end{pmatrix}$$
Références#
Ouvrage sur les fondamentaux du machine learning :
- É. Biernat et M. Lutz, Data Science : Fondamentaux et études de cas : Machine Learning avec Python et R, Eyrolles (2015)