J’apprécie beaucoup les arbres de décision et random forest pour leur simplicité d’interprétation. Ces modèles font partie des classiques en machine learning, très utilisés aussi bien pour la régression que pour la classification
Un point essentiel lorsqu’on construit un arbre de décision, c’est le choix de la mesure d’impureté pour évaluer la qualité d’un découpage à chaque nœud. Deux critères sont particulièrement courants : l’indice de Gini et l’entropie.
1. Arbres de décision#
1.1. Structure#
Un arbre de décision est un modèle d’apprentissage supervisé qui prend la forme d’une structure arborescente où :
- chaque nœud représente une décision fondée sur une variable (ou attribut),
- chaque branche correspond au résultat de cette décision,
- chaque feuille donne la classe cible (ou la valeur de sortie).
1.2. Comment ça marche ?#
Voici les grandes étapes de construction d’un arbre de décision :
Choix de l’attribut : l’algorithme commence par sélectionner la variable la plus discriminante pour séparer les données de façon aussi homogène que possible. Pour cela, il s’appuie sur des mesures comme Gini ou l’entropie – c’est cette étape qui nous intéresse ici.
Découpage des données : une fois l’attribut choisi, les données sont divisées en sous-groupes selon les valeurs de cette variable. Chaque valeur donne lieu à une branche.
Construction récursive : le processus est répété pour chaque sous-nœud, jusqu’à atteindre un critère d’arrêt (profondeur maximale, nombre minimal d’exemples, ou pureté totale du nœud).
Prédiction : une fois l’arbre construit, on peut l’utiliser pour faire des prédictions en suivant le chemin correspondant aux valeurs de l’observation.
Interprétation : l’un des gros avantages des arbres de décision, c’est leur lisibilité. On peut facilement retracer les décisions prises et identifier les variables les plus importantes.
2. Deux critères pour guider le découpage#
2.1 L’impureté de Gini#
L’impureté de Gini mesure la probabilité de mal classer un élément pris au hasard, en fonction de la répartition des classes dans un nœud. Plus les classes sont déséquilibrées, plus l’indice est faible – ce qui est bon signe pour la séparation.
La formule est la somme des carrés des probabilités de chaque classe :
$$\text{Gini Index} = 1 - \sum_j p_j^2$$
où \(p_j\) est la probabilité d’appartenir à la classe \(j\).
Quelques repères :
L’indice de Gini est minimum (= 0) lorsque le nœud est pur (tous les éléments sont de la même classe). $$ \text{Gini}_{\min} = 1 - (1^2) = 0 $$
Il est maximum (= 0.5) lorsque les classes sont équilibrées à 50/50. $$ \text{Gini}_{\max} = 1 - (0.5^2 + 0.5^2) = 0.5 $$
En pratique, on cherche à minimiser l’impureté pour trouver les meilleurs points de séparation.
2.2. L’entropie#
L’entropie mesure le désordre ou l’incertitude dans les données. Plus les classes sont équilibrées, plus l’entropie est élevée.
La formule est la somme des probabilités de chaque classe multiplié par le logarythme de ces probabilités :
$$\text{Entropy} = - \sum_j p_j \cdot \log_2 \cdot p_j$$
où \(p_j\) est la probabilité d’appartenir à la classe \(j\).
Comme pour Gini :
Minimum = 0 → nœud pur
$$ \text{Entropy}_{\min} = -1 \cdot \log_2(1) = 0 $$
Maximum = 1 → classes équilibrées à 50/50
$$ \text{Entropy}_{\max} = -0.5 \cdot \log_2(0.5)-0.5 \cdot \log_2(0.5) = 1 $$
Là encore, l’objectif est de réduire l’entropie pour obtenir des sous-groupes les plus homogènes possible.
3. Comparaison des deux critères#
Dans la pratique, les critères Gini et Entropie donnent souvent des résultats très proches, que ce soit en termes de structure d’arbre ou de performance prédictive. Le choix de l’un ou l’autre n’a donc rien de critique dans la majorité des cas. Cela dit, en creusant un peu (notamment via une étude détaillée publiée sur quantdare), on peut tout de même relever quelques différences intéressantes.
En pratique, Gini et Entropie donnent souvent des résultats similaires. Le choix entre les deux n’est pas toujours décisif, mais voici quelques différences intéressantes tirées d’un article de :
3.1 Échelle des valeurs#
Premier point : l’échelle sur laquelle varient les deux mesures :
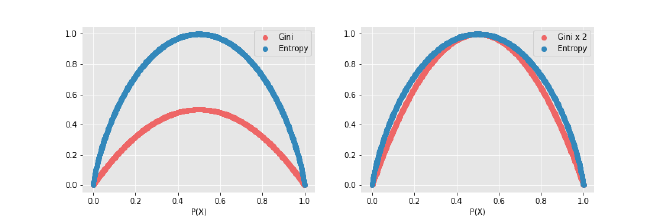
- L’indice de Gini varie de 0 à 0,5.
- L’entropie varie de 0 à 1.
Autrement dit, à première vue, l’entropie semble plus « étalée ». Mais si on multiplie les valeurs de Gini par 2, on obtient une courbe presque identique à celle de l’entropie. C’est une différence de forme, pas de fond, mais à garder à l’esprit si on veut comparer les métriques ou visualiser leur évolution.
3.2 Coût computationnel et temps d’entraînement#
Deuxième différence, plus concrète : le coût de calcul.
- Le critère Gini est plus léger à calculer, car il se contente de probabilités au carré.
- L’entropie implique des logarithmes, ce qui le rend un peu plus lourd et donc plus lent à exécuter.
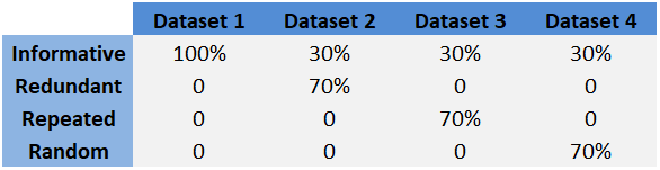
Pour vérifier cela, les auteurs de l’étude ont mené des analyses comparatives sur différents jeux de données synthétiques. Chaque dataset contenait 10 variables, mais leur nature variait :
- Informative : les variables apportent de la vraie information discriminante.
- Redondante : certaines variables sont des copies partielles d’autres.
- Répétée : certaines colonnes sont dupliquées sans ajout d’information.
- Aléatoire : bruit pur, sans relation avec la cible.
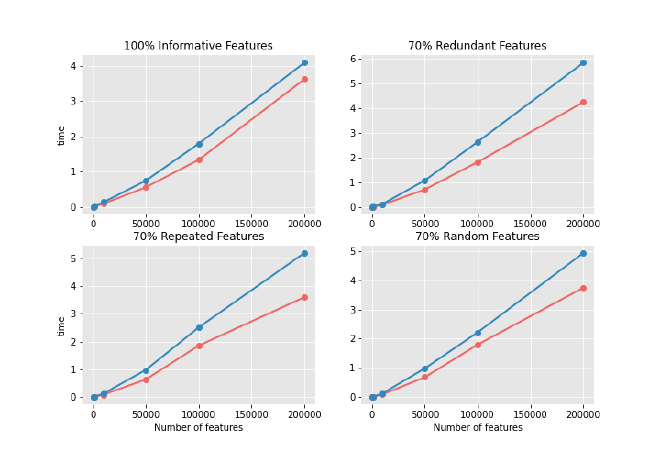
Pour chaque type, ils ont testé 5 tailles d’échantillons : 100, 1 000, 10 000, 100 000 et 200 000 exemples. De quoi bien observer l’impact du critère choisi sur les performances.
3.3 Résultats observés#
Sur les graphiques comparatifs, on voit que :
- Le temps d’apprentissage est systématiquement plus élevé avec l’entropie.
- Cet écart est d’autant plus marqué que le jeu de données est grand.
- Les variables redondantes ralentissent particulièrement l’apprentissage (jusqu’à +50 % de temps d’exécution par rapport à des variables vraiment informatives).
- Les variables aléatoires ou répétées produisent un effet similaire.
3.4 Et côté performance ?#
L’étude va encore un peu plus loin avec des analyses de validation croisée et des comparaisons des structures d’arbres générées. Résultat :
- Le critère Gini reste plus rapide et donc souvent préféré dans un contexte production.
- Le critère Entropie donne parfois des résultats légèrement meilleurs, mais l’écart est mince.
Conclusion#
Sauf cas très spécifiques ou contraintes très fines sur la précision, je recommande Gini : plus simple, plus rapide, presque aussi bon.