Organiser la diffusion d’un sondage peut rapidement devenir un casse-tête, surtout lorsqu’il faut jongler avec plusieurs contraintes. Heureusement, avec un peu de programmation linéaire et la bibliothèque PuLP en Python, on peut s’en sortir avec élégance.
1. Introduction#
1.1 La base de données initiale#
On part d’une base de données clients. Chaque ligne contient une adresse email, un secteur d’activité, et un fichier factice.
Dans ce jeu de données, un même individu (\(x_i\)) peut apparaître plusieurs fois, associé à différents secteurs (\(y\)) ou fichiers (\(z\)).
1.2 Les contraintes#
On souhaite construire un échantillon optimal de combinaisons (\(x\), \(y\), \(z\)), en respectant les règles suivantes :
- Pas de doublons : chaque combinaison doit être unique.
- Pas de redondance : un individu (\(x_i\)) ne doit apparaître qu’une seule fois. On ne veut pas envoyer plusieurs enquêtes à la même personne.
- Équilibre sectoriel : on cherche une répartition aussi homogène que possible entre les différents secteurs (\(y\)).
2. Programmation linéaire et bibliothèque PuLP#
La programmation linéaire est une méthode mathématique qui permet de trouver la meilleure solution possible (solution optimale) à un problème soumis à des contraintes précises.
L’idée est simple :
- on définit les contraintes à respecter,
- une fonction objectif (par exemple, maximiser l’équilibre, minimiser les doublons),
- et on laisse un solveur trouver la combinaison qui satisfait tout ça au mieux.
C’est là que PuLP entre en jeu. Cette bibliothèque Python nous permet de modéliser ce genre de problème très facilement :
- on définit des variables de décision,
- on fixe les contraintes,
- on précise la fonction à optimiser.
Et le tour est joué.
PuLP est un outil à la fois puissant, lisible, et surtout reproductible. Parfait pour générer un échantillon d’enquête équilibré.
3. Étapes de traitement#
3.1. Préparation des données#
Avant d’attaquer la modélisation avec PuLP, il faut préparer nos données. Cette étape consiste à :
- Charger les données depuis un fichier CSV contenant les colonnes essentielles : adresse email, secteur d’activité, et fichier d’enquête associé.
- Anonymiser les données sensibles, notamment les adresses email et les noms de fichiers, en les “hachant” avec une fonction de hash (ici hash_string). Cela permet de garantir la confidentialité tout en conservant des identifiants uniques.
- Extraire les listes uniques de chaque dimension (emails, secteurs, fichiers), qui serviront plus tard à construire nos variables de décision.
- Générer les combinaisons existantes de type (email, secteur, fichier) à partir des lignes du jeu de données.
Voici le code correspondant à cette étape :
import pandas as pd
import hashlib
# load
data = pd.read_csv("data.csv", usecols=["email", "sector","file"])
# hash
data['email'] = data['email'].apply(hash_string)
data['file'] = data['file'].apply(hash_string)
# unique lists of emails, channels and folders
emails = data['email'].unique()
sectors = data['sector'].unique()
files = data['file'].unique()
# list of tuples (x, y, z)
combinations = [(row['email'], row['sector'], row['file']) for _, row in data.iterrows()]
3.2. Préparation du problème d’optimisation#
Maintenant que nos données sont prêtes, passons à l’étape clé : la modélisation du problème d’optimisation.
L’objectif ici est de sélectionner un sous-ensemble optimal de combinaisons (email, secteur, fichier) en respectant plusieurs contraintes :
- Pas de doublons (chaque email et chaque fichier ne doivent apparaître qu’une seule fois),
- Répartition équilibrée des secteurs,
- Nombre total de combinaisons sélectionnées aussi élevé que possible.
Pour ça, on utilise PuLP, qui permet de formuler et résoudre un problème de programmation linéaire.
Voici les grandes étapes du code :
from pulp import LpMaximize, LpProblem, LpVariable, lpSum, LpMinimize, PULP_CBC_CMD
prob = LpProblem("Optimize_Combinations", LpMaximize)
# Decision variables: 1 if the combination is chosen, 0 otherwise
decision_vars = LpVariable.dicts("Choose", combinations, cat='Binary')
# Auxiliary variables for balancing
sector_count_vars = {sector: LpVariable(f"Count_{sector}", cat='Integer', lowBound=0) for sector in sectors}
max_sector_count = LpVariable("Max_Sector_Count", cat='Integer', lowBound=0)
min_sector_count = LpVariable("Min_Sector_Count", cat='Integer', lowBound=0)
Contraintes#
- Un email ne peut être sélectionné qu’une seule fois
→ On veut éviter de solliciter plusieurs fois la même personne.
# 1. Each email must appear only once
for email in emails:
prob += lpSum([decision_vars[(x, y, z)] for (x, y, z) in combinations if x == email]) <= 1
- Un même fichier ne peut être utilisé qu’une seule fois
→ On suppose ici que chaque fichier d’enquête est unique pour une combinaison.
# 2. Each file must appear only once
for file in files:
prob += lpSum([decision_vars[(x, y, z)] for (x, y, z) in combinations if z == file]) <= 1
- Calcul du nombre de sélections par secteur
→ Ces variables vont nous permettre de suivre combien de fois chaque secteur est représenté.
# 3. Track the number of times each sector is selected
for sector in sectors:
prob += sector_count_vars[sector] == lpSum([decision_vars[(x, y, z)] for (x, y, z) in combinations if y == sector])
- Équilibrage des secteurs sélectionnés
→ On introduit une contrainte pour forcer les secteurs à être répartis de façon équilibrée, en limitant l’écart entre le secteur le plus représenté et le moins représenté.
# 4. Defining constraints to balance sectors
for sector in sectors:
prob += max_sector_count >= sector_count_vars[sector]
prob += min_sector_count <= sector_count_vars[sector]
Fonction objectif#
Enfin, on définit ce que l’on cherche à optimiser.
Ici on veut :
- maximiser le nombre total de combinaisons sélectionnées,
- tout en minimisant l’écart entre les secteurs les plus et les moins représentés.
C’est un compromis entre quantité et équilibre :
# Objective function: maximise the number of combinations chosen while minimising the gap between the sectors
prob += lpSum([decision_vars[comb] for comb in combinations]) - (max_sector_count - min_sector_count)
Dans la réalité, ce n’est pas toujours possible (ex : trop peu d’individus dans un secteur). C’est pourquoi on cherche ici à réduire l’écart entre les secteurs, sans imposer une égalité stricte.
3.3. Résolution du problème#
Une fois notre problème d’optimisation modélisé, il ne reste plus qu’à le résoudre :
prob.solve(PULP_CBC_CMD())
Ici, on utilise PULP_CBC_CMD(), le solveur par défaut de PuLP. CBC (pour Coin-or Branch and Cut) est un algorithme de résolution de problèmes de programmation linéaire développé par le projet COIN-OR (Computational Infrastructure for Operations Research).
Il repose sur une combinaison de deux techniques issues de la recherche opérationnelle :
Branch-and-Bound (séparation et évaluation, qui explore intelligemment les solutions possibles) C’est une méthode d’exploration intelligente des solutions possibles dans un problème combinatoire.
- Le principe : on divise progressivement l’espace des solutions en sous-espaces (c’est le branching), un peu comme si on construisait un arbre de décisions.
- Pour chaque sous-espace, on calcule une borne optimale (minimale ou maximale) qu’on pourrait atteindre.
- Si cette borne est moins bonne que ce qu’on a déjà trouvé ailleurs, on abandonne ce sous-espace (c’est le bounding).
Cela permet d’éviter d’explorer toutes les possibilités une à une : seules les branches prometteuses sont poursuivies.
Cutting Planes (plans de coupe, qui éliminent des zones non pertinentes du champ de recherche) Les plans de coupe viennent en renfort du branch-and-bound, notamment dans les problèmes entiers (où les variables doivent valoir 0 ou 1, comme ici).
- Lorsqu’une solution optimale trouvée est “fractionnaire” (ex. choisir un fichier à 0,5 au lieu de 0 ou 1), ce n’est pas une solution valide.
- Les plans de coupe ajoutent alors des contraintes supplémentaires au problème pour exclure cette solution irréaliste tout en gardant les solutions entières valides.
On affine ainsi l’espace des solutions, en le resserrant autour des solutions admissibles.
En combinant ces deux approches, CBC est capable de résoudre efficacement des problèmes d’optimisation comme le nôtre, avec des milliers de variables binaires et des contraintes d’équilibre.
Ce solveur est rapide, fiable et open source, parfait pour ce genre de problème.
3.4. Extraction des combinaisons retenues#
Une fois la résolution effectuée, on peut extraire les combinaisons sélectionnées :
chosen_combinations = [(x, y, z) for (x, y, z) in combinations if decision_vars[(x, y, z)].varValue == 1]
results_df = pd.DataFrame(chosen_combinations, columns=['email', 'sector', 'file'])
Ce DataFrame contient donc l’échantillon optimisé : une seule ligne par email, une seule ligne par fichier, et une distribution équilibrée des secteurs.
3.5. Résultats#
Une visualisation rapide permet de constater l’effet de notre optimisation. Par exemple, la répartition par secteur :
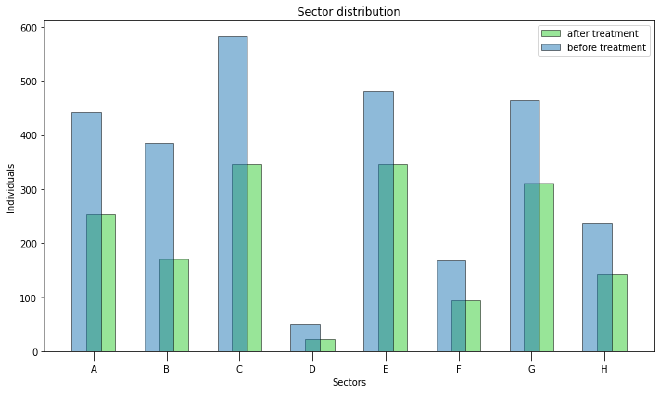
On voit que la distribution est bien plus homogène que dans les données brutes. Chaque contact est sollicité une seule fois, et les secteurs sont représentés équitablement.
4. Quelques remarques#
Le script s’exécute en moins d’une seconde pour une base de données de 3000 lignes.
La solution est propre, interprétable et, surtout, facile à reproduire, y compris en ajoutant d’autres contraintes si nécessaire.
Si le concept vous intéresse, d’autres problèmes courants ont été résolus à l’aide de cet algorithme, et vous trouverez ici quelques présentations sympas.