Valeurs manquantes et valeurs aberrantes

Quand on travaille avec des données réelles, on se rend compte qu’elles sont rarement parfaites. Il manque des valeurs, certaines semblent étranges, d’autres carrément hors cadre.

Cet article fait le point sur deux grands classiques de la statistique appliquée : les valeurs manquantes et les valeurs aberrantes. L’objectif est de comprendre ce qui se cache derrière ces situations, pourquoi elles posent problème, et les différentes manières de les traiter.

Les valeurs manquantes : pas toutes manquantes pour les mêmes raisons

#

Avant de chercher à corriger des valeurs manquantes, il faut déjà comprendre pourquoi elles sont absentes. Little et Rubin (2002) proposent une classification très utilisée, basée sur les mécanismes qui génèrent ces données manquantes.

MCAR – Missing Completely At Random

#

Ici, les données manquent complètement au hasard. La probabilité qu’une valeur de la variable \(X_1\) soit manquante ne dépend ni des autres variables observées, ni de celles qui sont elles-mêmes manquantes.

Autrement dit : il n’existe aucun profil particulier d’individus avec des données manquantes. Chaque observation a la même probabilité d’être incomplète. C’est le cas le plus confortable… et aussi le plus rare en pratique.

MAR – Missing At Random

#

Dans ce cas, les données manquantes ne sont pas totalement dues au hasard, mais elles restent explicables par ce qu’on observe. La probabilité qu’une valeur de \(X_1\) soit manquante dépend d’autres variables observées, mais pas de la valeur manquante elle-même.

Par exemple, un revenu manquant peut dépendre de l’âge ou du niveau d’étude (connus), mais pas du revenu réel (inconnu). C’est une situation très fréquente en analyse de données.

MNAR – Missing Not At Random

#

Ici, on entre dans le cas le plus délicat. La donnée est manquante pour une raison directement liée à sa valeur réelle, qui n’est justement pas observée.

Par exemple, des individus aux revenus très élevés (ou très faibles) choisissent de ne pas répondre à la question. La probabilité d’avoir une valeur manquante dépend donc de la valeur manquante elle-même.

Les données MNAR sont particulièrement problématiques, car elles introduisent des biais potentiellement forts dans les analyses.

En pratique, il est très difficile de déterminer avec certitude si les données sont MCAR, MAR ou MNAR. On fait donc souvent ce choix par hypothèse, en s’appuyant sur la connaissance métier et le contexte de collecte.

Avant de corriger, il faut décrire

#

Avant toute méthode de traitement, il est essentiel de prendre le temps d’explorer les données manquantes :

• Quel est le pourcentage de valeurs manquantes par variable ?
• Certaines populations ou certains groupes sont-ils plus touchés que d’autres ?
• Existe-t-il des variables observées qui semblent prédire la présence de données manquantes ?

Cette étape est souvent sous-estimée, alors qu’elle conditionne directement la pertinence des méthodes utilisées ensuite.

Comment traiter les valeurs manquantes ?

#

Il n’existe pas de méthode universelle. En pratique, on teste souvent plusieurs approches, et on observe leur impact sur les résultats. Cela implique des allers-retours réguliers entre les données brutes et les données corrigées.

Voici un panorama des méthodes les plus courantes.

Analyse sur données complètes

#

C’est la méthode la plus simple : on ne conserve que les observations sans aucune valeur manquante.

Elle peut être acceptable si les individus concernés représentent moins de 5 % de la population. Au-delà, le risque de perte d’information et de biais devient important.

Imputation par règle métier

#

Quand on dispose de règles métiers solides, on peut parfois calculer une valeur manquante à partir d’autres informations disponibles.

Cette approche est très pertinente lorsqu’elle repose sur une logique claire et validée, mais elle reste limitée à des cas bien spécifiques.

Remplacement par une statistique simple

#

On peut remplacer les valeurs manquantes par :

• la moyenne (variables quantitatives),
• la médiane,
• le mode ou la modalité la plus fréquente (variables qualitatives).

Ces méthodes sont faciles à mettre en œuvre, mais elles réduisent artificiellement la variabilité des données.

Imputation par ratio ou par régression

#

Ici, la valeur manquante est estimée à partir d’un modèle :

• un ratio simple,
• une régression linéaire,
• ou des méthodes plus complexes comme les forêts aléatoires.

Ces approches donnent souvent de meilleurs résultats, mais elles peuvent renforcer artificiellement certaines relations entre variables.

Méthodes hot-deck et cold-deck

#

Le principe est de remplacer une valeur manquante par une valeur observée chez un autre individu :

• Hot-deck : le tirage se fait dans le jeu de données analysé.
• Cold-deck : le tirage se fait dans une source de données externe (rare en pratique, notamment en machine learning).

Méthode du plus proche voisin

#

Proche du hot-deck, mais plus ciblée : la valeur est tirée chez des individus aux caractéristiques similaires, définies via une mesure de distance.

Imputation multiple

#

L’imputation multiple cherche justement à mieux représenter cette incertitude.

Le principe :

1. Chaque valeur manquante est remplacée par \(M>1\) valeurs plausibles.
2. On réalise la même analyse sur chacune des \(M\) bases imputées.
3. Les résultats sont ensuite combinés pour produire un estimateur unique.

Dès \(M=5\), on obtient généralement de bons résultats. L’objectif n’est pas de prédire parfaitement les valeurs manquantes, mais de préserver les distributions et les relations entre variables.

Plusieurs algorithmes existent :

• EM (Expectation - Maximisation),
• MCMC (Méthode de Monte-Carlo par chaînes de Markov),
• PMM (Predictive Mean Matching).

Variable indicatrice de valeur manquante

#

Pour les variables catégorielles, on peut créer une modalité spécifique correspondant aux valeurs manquantes.

Cela permet de mesurer directement l’effet du fait d’avoir une donnée manquante et d’évaluer le risque de biais associé.

Correction par pondération

#

En cas de non-réponse totale ou partielle, on peut ajuster des poids sur les individus ou les variables afin de rééquilibrer le jeu de données.

Et en machine learning, on fait comment ?

#

En machine learning, les valeurs manquantes posent exactement les mêmes questions… avec souvent encore moins de tolérance à l’improvisation.

Beaucoup d’algorithmes classiques (régressions, SVM, réseaux de neurones, k-means, etc.) ne savent tout simplement pas gérer les valeurs manquantes. Sans pré-traitement, l’entraînement du modèle est impossible.

D’autres méthodes, comme certains arbres de décision ou algorithmes de type gradient boosting, peuvent intégrer les valeurs manquantes de manière plus ou moins native. Mais cela ne signifie pas pour autant que le problème disparaît : le mécanisme de données manquantes influence toujours le modèle appris.

Dans tous les cas, le choix du traitement des valeurs manquantes a un impact direct sur les performances, la stabilité et l’interprétabilité des modèles. Une imputation trop naïve peut artificiellement améliorer les scores, tout en dégradant la capacité de généralisation.

Là encore, il n’existe pas de solution universelle : on teste, on compare, et on garde en tête que le pré-traitement fait pleinement partie du modèle.

Les valeurs aberrantes : erreurs ou signaux faibles ?

#

Autre situation courante : les valeurs aberrantes, aussi appelées outliers statistiques.

Une valeur aberrante est une valeur extrême qui diffère significativement du reste de la distribution d’une variable. Elle se situe loin du « cœur » des données, sans pour autant être automatiquement une erreur.

On les identifie souvent à l’aide de boxplots (boîtes à moustaches), qui reposent sur la notion de quartiles et d’écart interquartile.

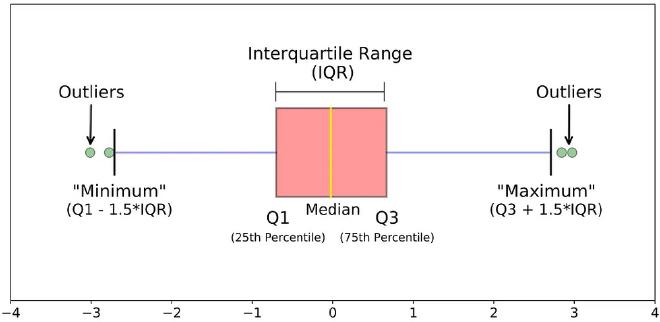
L’écart interquartile, noté \(IQR\), mesure la dispersion des 50 % centraux des données :

\[ IQR = Q3 - Q1 \]

où :

• \(Q1\) est le premier quartile (25 % des données en dessous),
• \(Q3\) est le troisième quartile (75 % des données en dessous).

À partir de cet écart interquartile, on définit deux bornes :

• borne inférieure :
  \[ Q1 - 1{,}5 \times IQR \]

• borne supérieure :
  \[ Q3 + 1{,}5 \times IQR \]

Toute valeur :

• plus petite que la borne inférieure,
• ou plus grande que la borne supérieure,

est alors considérée comme une valeur aberrante (outlier).

Sur un boxplot :

• la boîte représente l’intervalle \([Q1, Q3]\),
• le trait à l’intérieur de la boîte correspond à la médiane,
• les moustaches s’étendent jusqu’aux valeurs les plus extrêmes restant à l’intérieur des bornes,
• les points isolés, situés au-delà des moustaches, correspondent aux valeurs aberrantes.

Le facteur \(1{,}5\) est une convention largement utilisée, introduite par Tukey. Il ne s’agit pas d’une règle universelle, mais d’un compromis pratique pour détecter des valeurs atypiques sans être trop sensible au bruit.

Que faire avec une vraie valeur aberrante ?

#

Si la valeur est jugée réellement problématique, on peut limiter son impact en utilisant certaines des méthodes d’imputation vues précédemment.

En conclusion

#

Les valeurs manquantes et aberrantes font partie du quotidien de l’analyse de données. Les ignorer est rarement une bonne idée, mais les corriger sans réflexion peut être encore pire.

L’essentiel reste de comprendre le contexte, de tester plusieurs approches, et de toujours garder un œil critique sur l’impact des traitements appliqués.

Références

#

• Roderick J. A. Little, Donald B. Rubin - Statistical Analysis with Missing Data