Aujourd’hui, je me penche sur le célèbre concours Kaggle du Titanic. Même s’il est devenu un grand classique, ce challenge reste une excellente façon de pratiquer sur des données claires, bien structurées, et facilement accessibles. Rien de révolutionnaire ici, mais c’est parfait pour se remettre dans le bain — ou tout simplement pour s’amuser un peu avec les bases.
1. Statistiques descriptives sur les données brutes#
Le concours met à disposition deux jeux de données :
train(891 lignes, 11 variables)test(418 lignes, 10 variables)
À première vue, ces datasets sont bien organisés, simples à utiliser, et assez intuitifs.
Voici un aperçu des variables proposées (le détail complet est disponible sur la page du concours Kaggle) :
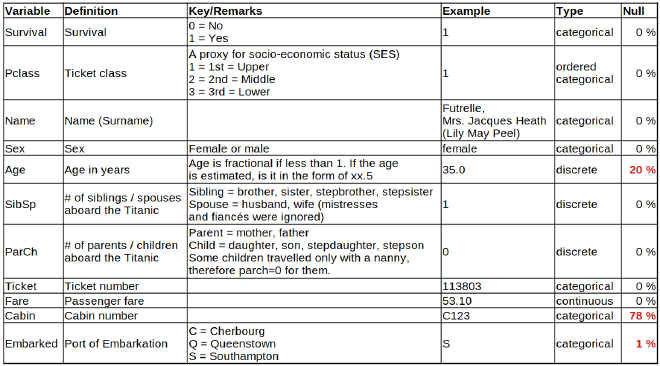
Je commence par explorer les variables une par une avec des statistiques descriptives de base. Le but ici est de comprendre rapidement la nature des données, leur distribution, la présence d’outliers, de valeurs manquantes, etc.
On ne compte que 11 variables, bien remplies dans l’ensemble, avec peu de valeurs manquantes. Parfait pour commencer sans passer trop de temps à nettoyer.
2. Nettoyage des données & feature engineering#
2.1. Création de nouvelles variables#
“En data science, 80 % du temps est consacré à la préparation des données, et 20 % à râler parce qu’il faut préparer les données.”
Sur Kaggle, les datasets sont souvent déjà bien nettoyés, mais on peut pousser encore plus loin, et c’est d’ailleurs un des côtés intéressants : un bon modèle, ça commence par des variables bien pensées. L’objectif est alors de maximiser l’information utile sans rien gâcher.
| Variable | Type | Définition | |
|---|---|---|---|
Survival | catégorique | C’est la variable cible \(y\) à prédire. | |
Pclass | ordonnée | Utilisable en l’état | |
Name | catégorique | Semble être structuré comme : name1, title, name2, name3 (nickname) | |
Title | catégorique | Créée à partir de Name : Mr, Mrs, Miss | |
HasNickname | catégorique | Créée à partir de Name, s’il a un surnom ou pas | |
Sex | catégorique | OK tel quel | |
Age | continue | Imputation des valeurs manquantes avec la médiane par Title | |
IsChild | catégorique | Créée à partir de Age : 1 si âge < 7 ; 0 sinon | |
AgeGroup | catégorique | Classe par tranche de 10 ans | |
SibSp | discrète | Frère et sœur | |
ParCh | discrète | Lien de parenté | |
IsAlone | catégorique | 1 si pas de parent ni frère/sœur | |
IsFamily | catégorique | 1 si présence d’au moins un proche | |
FamilySize | discrète | SibSp + ParCh + 1 | |
Ticket | catégorique | Structure du type : bureau de vente + numéro | |
TicketText | catégorique | première partie si texte | |
TicketNumber | catégorique | deuxième partie si numérique | |
HasFriend | catégorique | détecte des proches via des numéros de ticket proches | |
Fare | continue | Imputation des valeurs manquantes par médiane selon Title | |
FareByPerson | continue | Fare / FamilySize | |
Cabin | catégorique | Structure : Deck, CabinNumber | |
Deck | catégorique | première lettre de Cabin (ou -1 si NA) | |
CabinNumber | catégorique | numéro de cabine (ou -1 si NA) | |
Embarked | catégorique | Remplissage des valeurs manquantes par la catégorie la plus fréquente |
2.2. Suppression des variables devenues inutiles#
Certaines variables d’origine ne sont plus utiles après transformation :
NameCabinTicketTicketTextTicketNumber
2.3. Dataset intermédiaire#
Après nettoyage et enrichissement, on obtient un jeu de données avec 17 variables explicatives catégorielles, prêtes à être utilisées pour la modélisation.
3. Analyse exploratoire des données (EDA)#
3.1. Analyse univariée#
On formule quelques hypothèses métier.
Quels profils de passagers ont eu plus de chances de survivre ? Quels facteurs semblent importants ? L’exploration permet d’y voir plus clair.
Je reprends donc mes nouvelles variables nettoyées, et j’en examine les statistiques descriptives.
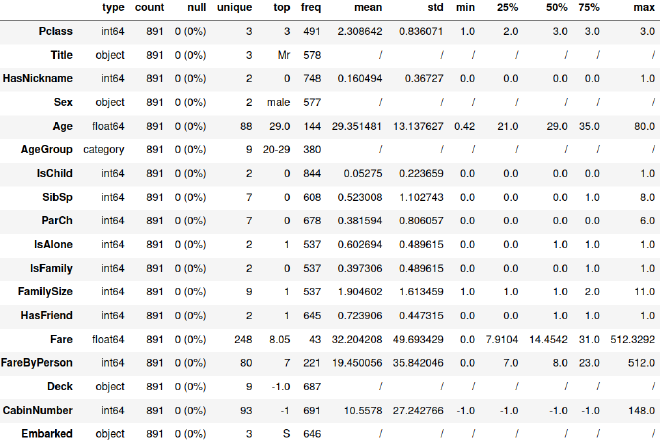
Puis quelques distributions des variables indépendantes :
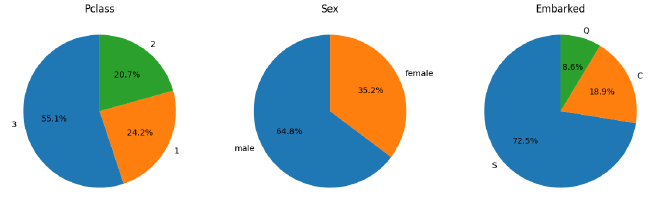
Pclass, Sex et Embarked

IsChild, IsAlone et HasFriend
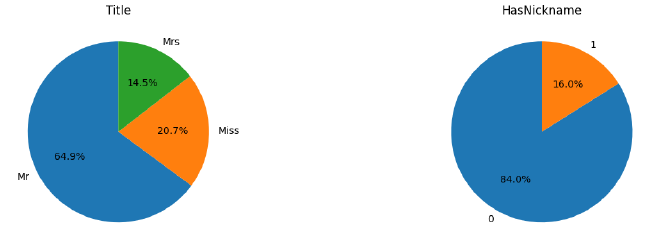
Title et HasNickname
3.2. Analyse bivariée#
Ensuite, j’analyse les relations entre chaque variable explicative et la variable cible \(y\) : Survived.
- Premier élément marquant : un tarif de 512£ pour une seule personne attire mon attention.
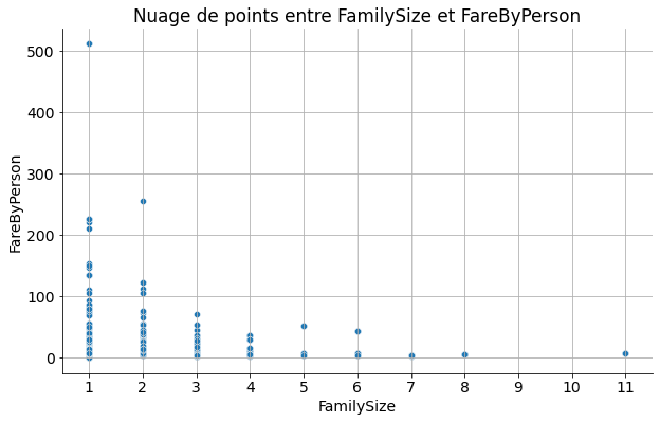
FareByPerson en fonction de FamilySize
Après vérification, il s’agit en fait d’une erreur sur les liens familiaux : c’était bien une famille, répartie sur trois cabines différentes, mais avec un seul ticket acheté.
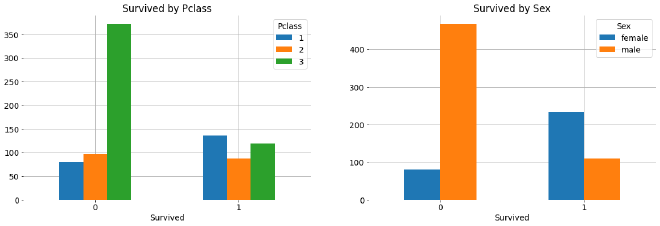
Survived par Pclass et Sex
Les premiers effets nets apparaissent :
- Les femmes en 1ʳᵉ classe ont des taux de survie bien supérieurs
- Les hommes en 3ᵉ classe, sans surprise, sont les plus défavorisés.
- Tests d’indépendance (chi²)
3.3. Analyse multivariée#
- Matrice de corrélation
- PCA, FCA, MCA
4. Prétraitement des données#
Avant de passer au machine learning, il faut finaliser le dataset. Je procède en deux temps :
- Encodage des variables catégorielles : je crée des variables indicatrices (dummies) 0/1 pour toutes les variables catégorielles.
Cela permet aux algorithmes de les traiter correctement, sans supposer d’ordre entre les catégories. - Normalisation des variables numériques : indispensable pour éviter que certaines variables (comme le tarif) ne dominent les autres.
Résultat : toutes les variables de mon jeu de données final sont numériques. On obtient une matrice d’entraînement \(X\) avec 41 variables prêtes à l’emploi.
5. Choix du modèle et validation croisée#
Vient ensuite la phase de modélisation. Je teste plusieurs algorithmes classiques de classification pour comparer leurs performances.
Voici le tableau récapitulatif des performances par algorithme :
| Classifier | Score |
|---|---|
| SVC | 0.826080 |
| XGBClassifier | 0.821610 |
| GradientBoostingClassifier | 0.812634 |
| LogisticRegression | 0.810325 |
| RandomForestClassifier | 0.809251 |
| AdaBoostClassifier | 0.798077 |
| BaggingClassifier | 0.792422 |
| KNeighborsClassifier | 0.786804 |
| DecisionTreeClassifier | 0.781199 |
| GaussianNB | 0.732896 |
Je décide de ne retenir que les modèles avec un score supérieur à 80%, histoire de rester exigeant. La suite consistera à affiner, combiner, ou améliorer ces modèles — mais ça, c’est pour la prochaine partie.
6. Prédictions et performances#
L’entraînement des différents modèles a produit des résultats assez homogènes, autour de 0,82 de score en validation croisée… sauf pour une méthode d’ensemble (stacking) qui a grimpé jusqu’à 0,91.
Mais attention, ce score ne reflète que la performance sur les données d’entraînement. En soumettant les prédictions sur Kaggle, la performance baisse : preuve que certains modèles surapprennent (overfitting).
Un score autour de 0,8 est considéré comme très bon sur cette compétition.
Voici les différences entre résultats de cross-validation et soumissions soumission sur Kaggle :
| Cross-Validation | Prediction | |
|---|---|---|
| RandomForestClassifier | 0.84 | 0.78 |
| LogisticRegression | 0.81 | 0.77 |
| GradientBoostingClassifier | 0.83 | 0.73 |
| XGBClassifier | 0.84 | 0.75 |
| SVC | 0.83 | 0.78 |
| Stacking | 0.92 | 0.78 |
Ce décalage rappelle l’importance de généraliser et non juste de performer sur l’échantillon d’apprentissage.
Et il faut rester lucide : le classement Kaggle est parfois biaisé par des participants ayant un accès détourné aux données de test finales. Difficile donc d’aller beaucoup plus haut qu’un score de 0,80 sans tricher.
Références et inspirations#
Pour progresser, j’ai consulté plusieurs sources utiles :
Kaggle competition
La compétition KaggleIbrahem Alhusseine - Titanic_model_with_98%_accuracy
Très bon travail de nettoyage et d’ingénierie, même si le train score élevé (98%) cache un test score décevant (74%) → typique d’un surapprentissage.É. Biernat et M. Lutz, Data Science : Fondamentaux et études de cas : Machine Learning avec Python et R, Eyrolles (2015)
Une méthodologie claire pour comprendre rapidement les logiques de modélisation.
Études et tests assez sympas et originaux :
- Titanic Ticket-only study
- Name-only study with interactive 3D plot
- Titanic “Spam” Filter
- Titanic using Name only [0.81818]
- Titanic WCG+XGBoost [0.84688]
- Divide and Conquer [0.82296]
- Titanic Top 4% with ensemble modeling
- Outlier!!! The Silent Killer
Certaines approches frisent l’absurde, d’autres sont brillantes — c’est aussi ce qui rend cette compétition amusante.
Le dataset complet (train + test + résultats) est disponible ici :